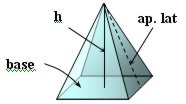
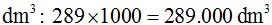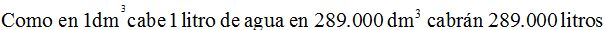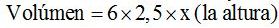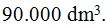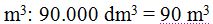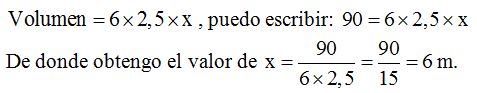VOLÚMENES DE LOS CUERPOS GEOMÉTRICOS
Para calcular un volumen necesitamos
tres dimensiones:
largo, ancho y alto. El producto de los valores
largo X ancho X alto nos da el
volumen.
Es lo mismo que decir, el volumen lo calculamos también multiplicando el área de la base por la altura.
Supongamos que tenemos unas cajas de cartón que tienen 1 cm., de largo, 1 cm. de ancho y 1 cm., de alto.
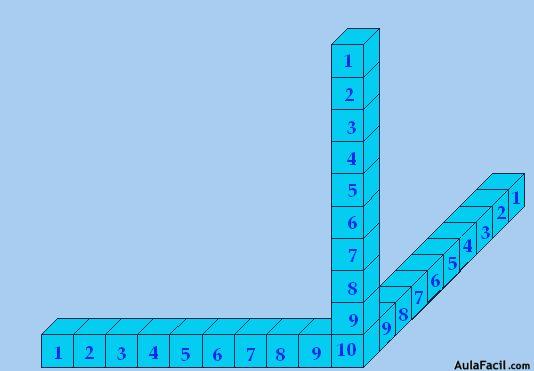
Las colocamos como aparecen en la siguiente figura:
Verás que hemos colocado las cajas en las tres dimensiones:
10 cajas de largo, 10 cajas de ancho y 10 de alto.
¿Cuántas cajas necesitamos para completar la superficie o la base?
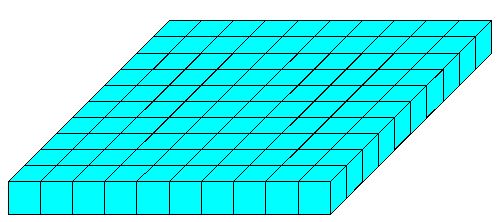
Según lo estudiado hasta ahora, nos harían falta: (largo por ancho) = 10x10=100 cajas que podemos observarlas en la siguiente figura ocupando el área de la base :
De otro modo: 10 filas de 10 cajas es igual a 100 cajas que son las que tienes en la figura.
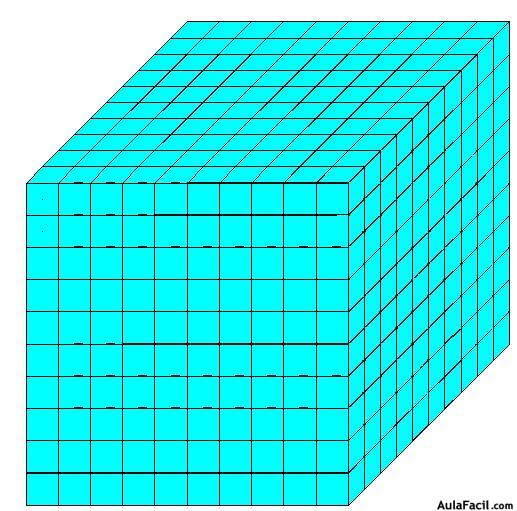
Si ahora completamos 10 capas como esta, colocándolas una encima de otra conseguiremos una altura de 10 cm.:
Una vez completadas las 10 filas de 100 cajas en la figura última tenemos 1000 cajas de 1 cm. de ancho, 1 cm., de largo y 1 cm., de alto.
Es muy importante que te fijes en que la última figura tiene 10 cm., de longitud, 10 cm., de anchura y 10 cm., de altura, lo que equivale a:
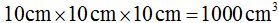
Recuerda que para multiplicar potencias de la misma base, sumamos los exponentes:
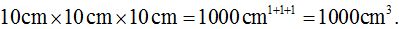
Vemos que el volumen de un cubo y de casi todas los cuerpos geométricos los calculamos multiplicando el área de la base por la altura.
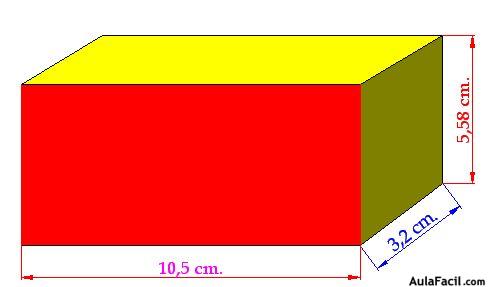
15(3).1 ¿Cuántas cajas pequeñas enteras de 1 cm. de largo, 1 cm. de ancho y 1 cm. de alto caben en la caja cuyas medidas aparecen en la siguiente figura?:
Respuesta: 187 cajas.
Solución
Calculo el volumen multiplicando las tres medidas: base por anchura, por altura y obtengo un resultado de
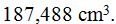
Cada caja tiene un volumen de
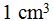
.
Como han de ser cajas enteras, la respuesta será 187 cajas.
15(3).2 En una caja grande de base rectangular han entrado 300 cajas pequeñas exactas de
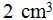
de volumen. La altura de la caja es de 10 cm. ¿Cuál es el área de la base?
Respuesta: 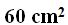
Solución
En primer lugar calculamos el volumen del recipiente o la caja grande. Para ello, nos dicen que caben 300 cajas pequeñas de
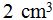
cada una. Esto quiere decir que el volumen del recipiente es de:
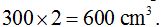
Sabemos que el volumen calculamos multiplicando el área de la base por la altura:
Sustituyo por los valores numéricos que conozco:
15(3).3 ¿Cuántos litros de agua caben en un depósito cuyas medidas las tienes en la figura siguiente, sabiendo que en un recipiente de
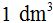
cabe exactamente 1 litro?
Respuesta: 289.000 litros de agua
Solución
Calculo el volumen del depósito:
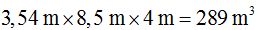
Este resultado lo escribo en
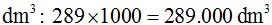
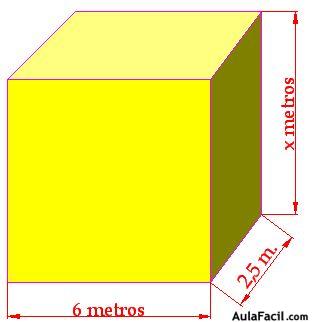
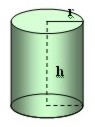
15(3).4 Halla la altura de un depósito que tiene por medidas las que ves en la figura siguiente. Sabemos que caben 90.000 litros de agua.
Respuesta: 6 m. de altura
Solución
Sabemos que el volumen obtenemos multiplicando las 3 dimensiones: largo, ancho y alto, es decir:
Conocemos el volumen porque nos dicen que caben 90.000 litros de agua.
Sabemos que 90.000 litros de agua equivalen a un volumen de
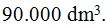
Dado que en el problema las medidas vienen dadas en metros, el volumen lo expresamos en
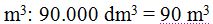
15(3).5 En un depósito caben 30.000 litros de agua. Tiene una altura de 3 metros ¿Cuál es el área de la base?
Respuesta: 10 metros cuadrados.
Figura
|
Esquema
|
Área
|
Volumen
|
| Cilindro |
| 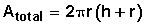 | 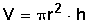 |
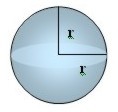
| Esfera |
| 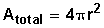 | 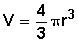 |
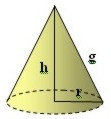
| Cono |
|  | 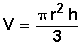 |
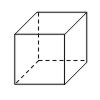
| Cubo |
|
A = 6 a2
|
V = a3
|
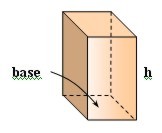
| Prisma |
|
A = (perim. base • h) + 2 • area base
|
V = área base • h
|
| Pirámide |
| 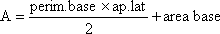 |  |
Poliedros regulares
Figura
|
Esquema
|
Nº de caras
|
Área
|
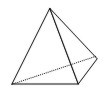
| Tetraedro |
| 4 caras, triángulos equiláteros | 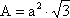 |
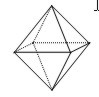
| Octaedro |
| 8 caras, triángulos equiláteros | 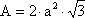 |
| Cubo |
| 6 caras, cuadrados | A = 6 a2 |
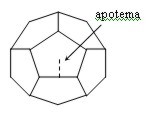
| Dodecaedro |
| 12 caras, pentágonos regulares | A = 30 · a · ap. |
| Icosaedro |
| 20 caras, triángulos equiláteros | 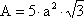 |




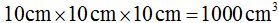
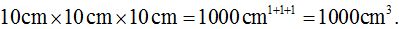
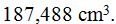
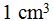 .
.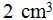 de volumen. La altura de la caja es de 10 cm. ¿Cuál es el área de la base?
de volumen. La altura de la caja es de 10 cm. ¿Cuál es el área de la base?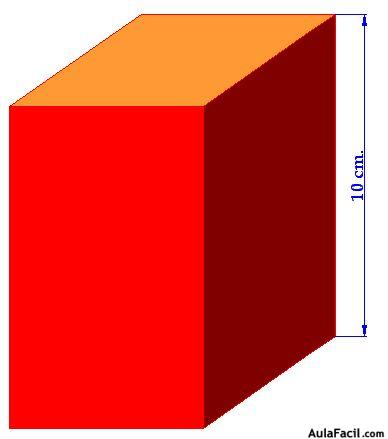
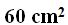
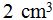 cada una. Esto quiere decir que el volumen del recipiente es de:
cada una. Esto quiere decir que el volumen del recipiente es de: 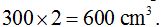
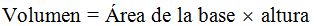
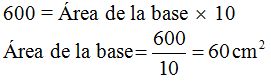
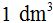 cabe exactamente 1 litro?
cabe exactamente 1 litro?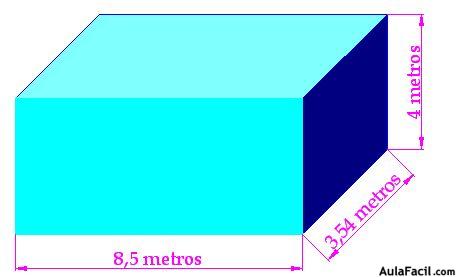
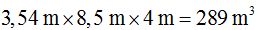 Este resultado lo escribo en
Este resultado lo escribo en